Version du 20 avril 2021
Algorithmes de tris¶
Matière à réfléchir I
Imaginez une bibliothèque scolaire un peu spéciale : les livres n’y sont pas rangés par ordre alphabétique ! Ils sont bien rangés sur des étagères, mais sans aucune logique particulière. Vous entrez dans cette bibliothèque un peu spéciale et vous vous mettez à chercher l’ouvrage Le Guide du voyageur galactique.
Pensez-vous pouvoir retrouver ce livre ?
Combien de temps cela vous prendrait-il ?
Y a-t-il des objets que vous rangez chez vous dans un ordre bien particulier ?
Algorithmes de tri classiques¶
Pour apprendre à cuisiner, on commence par suivre des recettes classiques. Ainsi, pour appréhender l’algorithmique, nous étudierons une classe d’algorithmes classiques : les algorithmes de tri.
Fig. 18 Trier. Des objets peuvent être triés selon une relation d’ordre, en lien avec une propriété. Sur la ligne du haut, les rectangles sont organisés selon leur couleur (de la plus sombre à la plus claire), alors que sur la ligne du bas, ils sont triés selon leur taille (du plus petit au plus grand).¶
Un algorithme de tri permet de trier des données, de les organiser selon une relation d’ordre. Dans la figure ci-dessus, les objets sont organisés soit par la luminosité de leur couleur, soit par leur taille, dans un ordre croissant.
Toutes les recettes de cuisine ne se valant pas, un algorithme peut aussi être plus adéquat qu’un autre algorithme. Il existe des dizaines d’algorithmes qui trient avec des approches différentes (nous en verrons quelques-uns). Certains sont plus rapides, d’autres moins gourmands en mémoire ou bien plus simples à coder. Ainsi, selon la situation, il faut choisir le bon algorithme.
Exercice 8
Trier les rectangles de la ligne du haut de la Figure Trier en fonction de leur taille (comme sur la ligne de bas). Représenter toutes les étapes intermédiaires par lesquelles vous passez avant d’arriver à la solution finale. Conseil : remplacer les rectangles par un nombre en lien avec leur taille.
En lien avec les ingrédients d’un algorithme, déterminer les données en entrée et le résultat en sortie de l’algorithme.
Quelles sont les opérations que vous avez effectuées ?
Solution de l’exercice 8
Tri par insertion¶
Voici l’algorithme du tri par insertion. Parcourir la liste d’éléments à trier du deuxième au dernier élément. Insérer chaque élément au bon emplacement de la liste déjà parcourue. Notez que la liste déjà parcourue (jusqu’à l’élément considéré à ce moment-là) est toujours bien triée.
Tri par sélection¶
L’algorithme du tri par sélection commence par rechercher le plus petit élément de la liste et l’échange avec le premier élément de la liste. Il recherche ensuite le plus petit élément de la liste restante, en excluant le nouveau premier élément, et l’échange avec le deuxième élément de la liste. Et ainsi de suite : il recherche le plus petit élément de la liste restante, en excluant les éléments déjà triés, et échange cet élément avec le premier élément pas encore trié. Il continue de la sorte jusqu’à ce que toute la liste soit triée.
Tri à bulles¶
L’algorithme du tri à bulles compare les éléments voisins. Commencer par comparer les deux premiers éléments de la liste et les mettre dans le bon ordre (le plus petit des deux éléments précède le plus grand). Comparer ensuite les deux éléments suivants (le nouveau deuxième et troisième élément de la liste) et les mettre dans le bon ordre. Continuer de la sorte jusqu’à la fin de la liste. Après ce premier parcours de la liste, le plus grand élément se retrouve en dernière position de la liste. Parcourir à nouveau la liste, en comparant et déplaçant les éléments voisins et en excluant le dernier élément qui est déjà bien trié. Parcourir la liste de la sorte, autant de fois qu’elle possède d’éléments, en excluant les éléments bien triés à la fin de la liste.
Exercice 9
[Résoudre cet exercice avant d’avancer dans le chapitre.] Appliquer un des trois algorithmes ci-dessus pour trier les rectangles de la ligne du haut de la Figure Trier en fonction de leur taille (le résultat est illustré dans la ligne du bas), en dessinant l’ordre des éléments à chaque fois qu’il change. Vous avez besoin d’une grande feuille de papier ou vous pouvez représenter la taille d’un rectangle par un nombre.
Solution de l’exercice 9
Le saviez-vous ? II
Pour trier 1 million d’éléments, selon l’algorithme choisi, cela peut prendre de l’ordre de 20 millions à 1 milliard d’opérations. Si chaque opération prend 1 microseconde (10-6 s) à s’exécuter, trier 1 million d’éléments pourrait prendre de 20 secondes (algorithme efficace) à 11 jours (pour un algorithme lent).
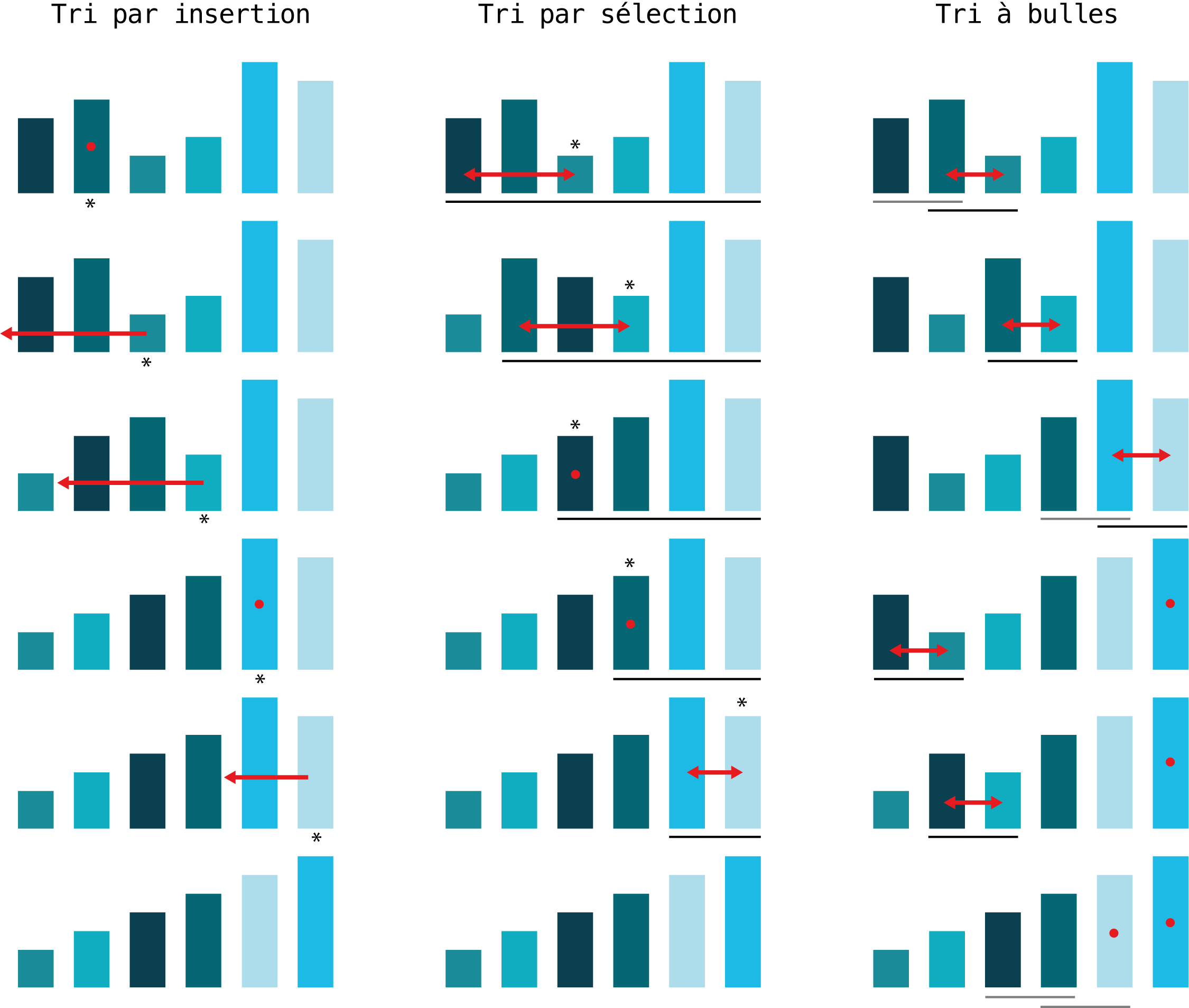
Fig. 19 Algorithmes de tri. Etapes intermédiaires lors de l’application des différents algorithmes de tri. La flèche rouge montre les mouvements des éléments suite à une opération. Si l’élément ne bouge pas, la flèche rouge est remplacée par un point rouge. A gauche, le tri par insertion. L’étoile dénote l’élément considéré à un moment donné. Au milieu, le tri par sélection. L’étoile désigne le plus petit élément de la liste non triée. A droite, le tri à bulles. Ici le point rouge signale les éléments triés.¶
Anecdote
Vous passez trop de temps à chercher vos affaires ? Pensez à mieux les ranger. Le temps perdu à ranger ses affaires est bien inférieur à celui que l’on passe à les chercher plus tard.
La figure ci-dessus détaille les étapes intermédiaires des trois algorithmes de tri vus précédemment. Dans le tri par insertion à gauche, on parcourt la liste dans l’ordre, un élément après l’autre (dénoté par une étoile). A chaque étape, on cherche à insérer le rectangle considéré à la bonne place dans la liste précédemment triée. La flèche rouge montre la position à laquelle le rectangle sera inséré. Si l’élément est déjà bien trié, aucune action n’est requise dans ce cas et la flèche est remplacée par un point rouge. Notez que la liste qui précède le rectangle considéré (celui avec l’étoile) est toujours bien triée.
Dans le tri par sélection au milieu, on parcourt la liste pour sélectionner son plus petit élément, et on le met à la bonne position. La ligne noire au‑dessous des rectangles montre la liste parcourue pour rechercher le plus petit élément. Le plus petit élément de cette liste est désigné par l’étoile. Finalement, la flèche rouge montre les éléments échangés : le premier élément de la liste non triée et le plus petit élément. Ainsi, le plus petit élément sélectionné (avec étoile) se retrouve à la fin de la liste déjà triée (liste non soulignée). Si l’élément est déjà bien trié et qu’aucune action n’est requise, la flèche bidirectionnelle est remplacée par un point rouge.
Dans le tri à bulles à droite, les lignes en dessous des rectangles montrent les éléments voisins qui sont comparés à chaque étape. Lorsque cette ligne est grise, les éléments sont déjà bien ordonnés et aucune action n’est requise. Lorsque la ligne est noire, les éléments ne sont pas dans le bon ordre et doivent être intervertis (flèche rouge). Après un passage complet de la liste, l’élément le plus grand se retrouve en dernière position, il remonte comme une bulle (voir la 4e ligne). Le point rouge ici indique les éléments triés. Dans ce cas, la liste est triée après deux parcours complets de la liste.
Notez que même si tous les algorithmes arrivent à la même solution finale, ils y arrivent de manière très différente et avec plus ou moins de calculs.
Exercice 10
Rappelez-vous la méthode que vous avez utilisée pour résoudre l’exercice 8. De quel algorithme de tri se rapproche-t-elle le plus ?
Solution de l’exercice 10
Exercice 11
Pour chaque algorithme, compter le nombre de comparaisons de la taille de deux éléments et le nombre de mouvements (rectangles déplacés).
Imaginons que ce qui prend le plus de temps est la comparaison. Dans ce cas précis, lequel des trois algorithmes faudrait-il utiliser ?
Imaginons que ce qui prend le plus de temps est le mouvement d’un élément. Dans ce cas précis, lequel des trois algorithmes serait le plus rapide ? Quel serait l’algorithme le plus lent ?
Solution de l’exercice 11
Le saviez-vous ? III
Il existe un algorithme, Bogosort, aussi nommé le tri lent ou encore le tri stupide. C’est un tri qui génère différentes permutations des éléments de la liste et s’arrête lorsque la configuration obtenue est par hasard triée. Combien d’opérations prend cet algorithme en moyenne ?
Comparaison d’algorithmes¶
La qualité d’un algorithme dépend de l’aspect que l’on souhaite optimiser (ou minimiser). Cela peut être la vitesse d’exécution (mesurée par le nombre d’instructions élémentaires exécutées), la place occupée en mémoire, ou encore le coût de certaines opérations comme le déplacement d’un élément. L’algorithme utilisé devrait être choisi en fonction de la situation.
La vitesse d’un algorithme dépend également des données en entrée. Selon la situation initiale des données en entrée (correspond à la ligne du haut de la Figure Algorithmes de tri), un algorithme « rapide » peut devenir « lent ». Il faut savoir que les algorithmes vus jusqu’ici sont des algorithmes lents, nous verrons un algorithme de tri rapide ultérieurement.
Aller plus loin
Imaginez que les quatre éléments d’une liste sont triés dans le sens inverse de ce que l’on souhaite (ils sont placés du plus grand au plus petit). Trier la liste selon les trois algorithmes de tri vus précédemment : le tri par insertion, le tri par sélection et le tri à bulles.
Dans cette configuration précise, quel algorithme est le plus rapide (présente le moins d’étapes intermédiaires) ? Quel algorithme est le plus lent ?
Exercices¶
Exercice 12
Réfléchir à votre journée : y a-t-il des actions qui se retrouvent chaque jour ouvrable ? Arrivez-vous à esquisser un algorithme que vous suivez sans que vous en ayez conscience ?
Exercice 13
Trier la liste [2,5,3,4,7,1,6] en utilisant les trois algorithmes de tri vus au cours. Représenter l’état de la liste après chaque étape qui change l’ordre des éléments.
Exercice 14
Ecrire un algorithme qui vérifie si une liste est triée.
Que prend l’algorithme en entrée et qu’est-ce qu’il retourne en sortie ?
Demander ensuite à un autre élève de suivre les opérations décrites par votre algorithme. Est-ce que votre algorithme est correct ?
Comparer vos algorithmes. Sont-ils différents ?
Exercice 15
Analyser les œuvres cubistes de Piet Mondrian. Trouver un algorithme qui permet de créer une œuvre qui pourrait être attribuée à Mondrian.
Ai-je compris ?
Je sais qu’il existe plusieurs manières différentes de résoudre un problème.
Je sais qu’il faut choisir le meilleur algorithme en fonction de critères objectifs : vitesse de l’algorithme, qualité de la solution, espace utilisé en mémoire ou encore consommation d’énergie.
Je sais appliquer les trois algorithmes de tri vus au cours.