Portes logiques¶
Exercice 3: portes logiques élémentaires
porte_ET
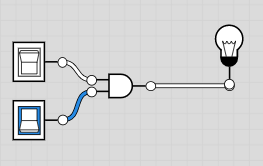
Porte logique ET
Compléter les tables de vérité suivantes pour les portes logiques ET, OU, NON et OU-X
ET (AND)
Nous avons la fonction A et B que nous notons: \(A·B\)
A |
B |
\(S=A·B\) |
|---|---|---|
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
OU (OR)
Nous avons la fonction A OU B que nous notons: \(A+B\)
A |
B |
\(S=A+B\) |
|---|---|---|
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
OU EXCLUSIF (OU-X, XOR)
Nous avons la fonction A ou B que nous notons: \(A \oplus B\)
A |
B |
\(S=A \oplus B\) |
|---|---|---|
0 |
0 |
|
0 |
1 |
|
1 |
0 |
|
1 |
1 |
NON (NOT)
Nous avons la fonction non A que nous notons: \(S= \overline{A}\)
| A | \(S= \overline{A}\) | |:—:|:—:|:—:| | 0 | | | 1 | |
Exercice 4: comparateur
Il peut être intéressant de disposer d’un moyen de comparer deux nombres. Une telle fonction retourne vrai (càd. 1) lorsque les deux nombres sont identiques.
Pour un seul bit, quelle porte ou combinaison de portes logiques permet d’assurer une telle fonction.
Pour un octet ou un demi-octet, comment assurer une telle fonction qui donnerait pour résultat vrai uniquement si tous les bits sont identiques.
Cette fonction relativement simple à réaliser est toujours présente dans les microprocesseurs. On peut cependant se représenter la complexité du circuit lorsque l’opération doit être implémentée pour des mots de 64 bits qui est la taille standard pour les microprocesseurs actuels
Exercice 5: lois de De Morgan
les lois de De Morgan proposent les égalités suivantes:
Que l’on peut aussi écrire avec un formalisme logique:
Et qui se formule en Francais:
La négation de la disjonction de deux propositions est équivalente à la conjonction des négations des deux propositions, ce qui signifie que « non(A ou B) » est identique à « (non A) et (non B) ».
La négation de la conjonction de deux propositions est équivalente à la disjonction des négations des deux propositions, ce qui signifie que « non(A et B) » est identique à « (non A) ou (non B) ».
On peut enfin en donner une représentation en diagramme de Venn.
DeMorgan
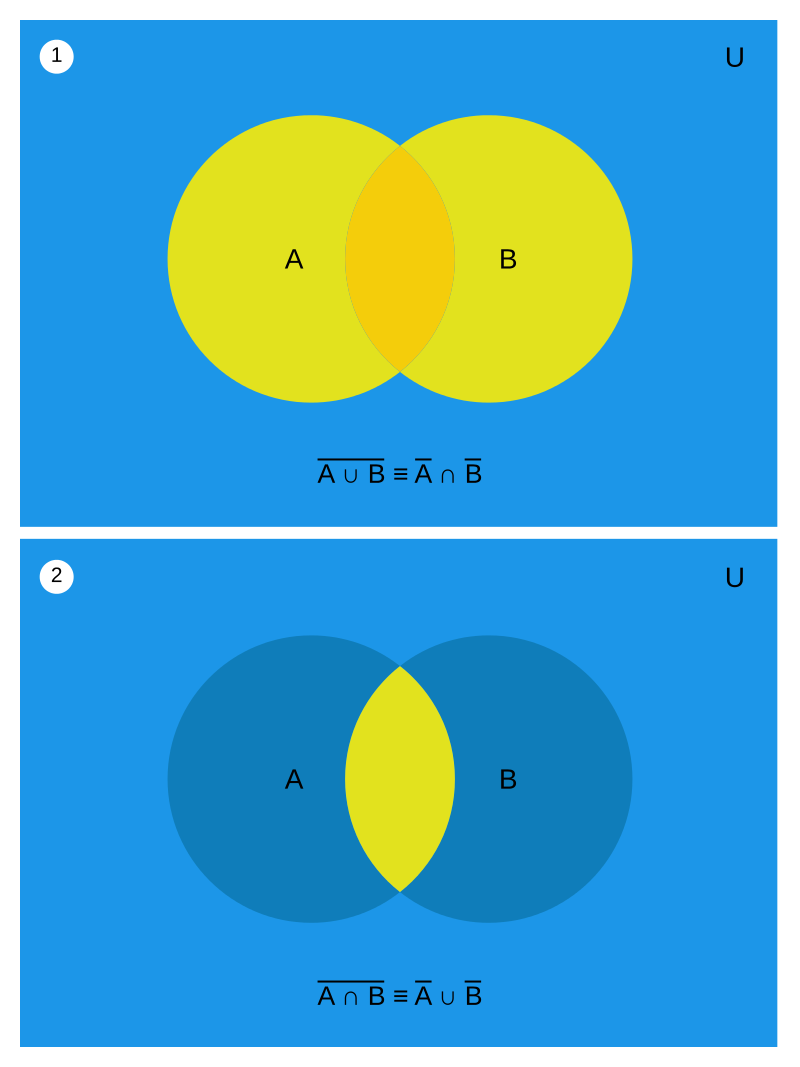
Diagrammes de Venn (source wikipedia2)
Consigne: Concevoir et mettre en place dans l’un ou l’autre des simulateurs un montage qui démontre le plus efficacement possible les lois de De Morgan.
En életronique digitale, ces lois sont remarquables parce qu’elles garantissent que l’on peut toujours remplacer des portes OU avec des portes ET (et inversément). Cette équivalence est abondamment utilisée dans la conception de circuits intégrés digitaux. Sachant que l’on peut également trouver une combinaison équivalente pour construire une porte OU-X et que l’on peut, en reliant ensemble les deux entrées d’une porte NON-ET en faire un inverseur (NON), on réalise que n’importe quel système de logique combinatoire peut-être réalisé avec uniquement des portes NON-ET.
- 2
Par Teknad — Travail personnel, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=36768081